Monte Carlo Tree Search

Sat Mar 10 2018

Series: Monte Carlo Tree Search

This blog post will discuss Monte Carlo tree search - one particularly powerful reinforcement learning technique that’s been employed in some of the most revolutionary game playing AI, including AlphaGo and AlphaZero. Before jumping right in though, we need to first cover the introductory topic of Game Trees.

Game Trees

The idea of a game tree is very straightforward. The nodes of a tree represent a state of the game. Edges of a node tell you what possible states can be reached from the current state.

A complete game tree contains every possible state of the given game. If you are able to build a complete game tree then it becomes trivial to calculate which moves are more likely to lead to a win. This is pretty easy to do in games that have a low average branching factor (the number of possible states reachable from the current one) and a low number of possible states

But what do we do when the number of possible states is high? Take Go as the quintessential example - this game has an estimated $10^{172}$ states. This is more possible board positions than atoms in the universe! No matter how powerful your computer is, you just can’t simulate enough moves to build a complete game tree. In fact, you’ll never even scratch the surface. So what do we do here? Enter the Monte Carlo tree search.

Monte Carlo Tree Search

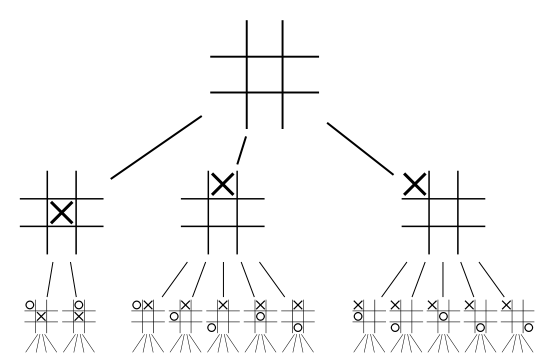
Imagine we have an AI that’s using Monte Carlo tree search (let’s call him HAL). HAL is plugged in to a game of tic-tac-toe and has been thinking about his first move. At the moment, HAL’s game tree looks like this:

First, let’s break this down. Each node has two values associated with it: $n$ and $w \!$ . $n$ represents the number of times this state has been considered, and $w$ represents the number of times the player who just played would have won from this position. That means that the $w$ in the darker nodes tell us how many times player X has won from that position and the $w$ lighter nodes tell us how many times player O has won from that position.

In most cases, we allow HAL a couple of seconds to make a decision. During that time, HAL thinks about what move he’d like to play. This is where the Monte Carlo tree search comes in.

Monte Carlo Tree search is made up of four distinct operations:

Selection
Expansion
Simulation
Backpropagation

HAL is going to keep cycling through these four phases for as long as he’s allowed to think. Each of these phases are covered in more detail below.

Selection

In the selection phase, we decide which action to think about taking. This is non-trivial - HAL doesn’t want to waste too much time thinking about taking bad moves, but he also doesn’t want to only consider moves that he feels good about because he might miss a big opportunity. This dilemma is referred to as the exploration/exploitation tradeoff.

Exploration refers to HAL thinking about moves that he hasn’t tried much already, where exploitation is taking advantage of HAL’s current knowledge and pushing it further. One of the most popular ways to balance these two goals is with the UCB1 formula. We choose the action that leads to the node for which the following equation is maximized.

\frac{w_i}{n_i} + c \sqrt{\frac{\ln N}{n_i}}

$w_i$ represents the number of wins considered for that node

$n_i$ represents the number of times that node has been considered (visit count)

$N$ represents the number of times all reachable nodes have been considered (sum of the visit count of all reachable nodes)

$c$ is a hyperparameter that we choose. The higher we set this hyperparameter, the more we value exploration over exploitation. This is typically set close to 1, but should be adjusted on a case-by-case basis.

If any nodes tie, we can choose between them at random.

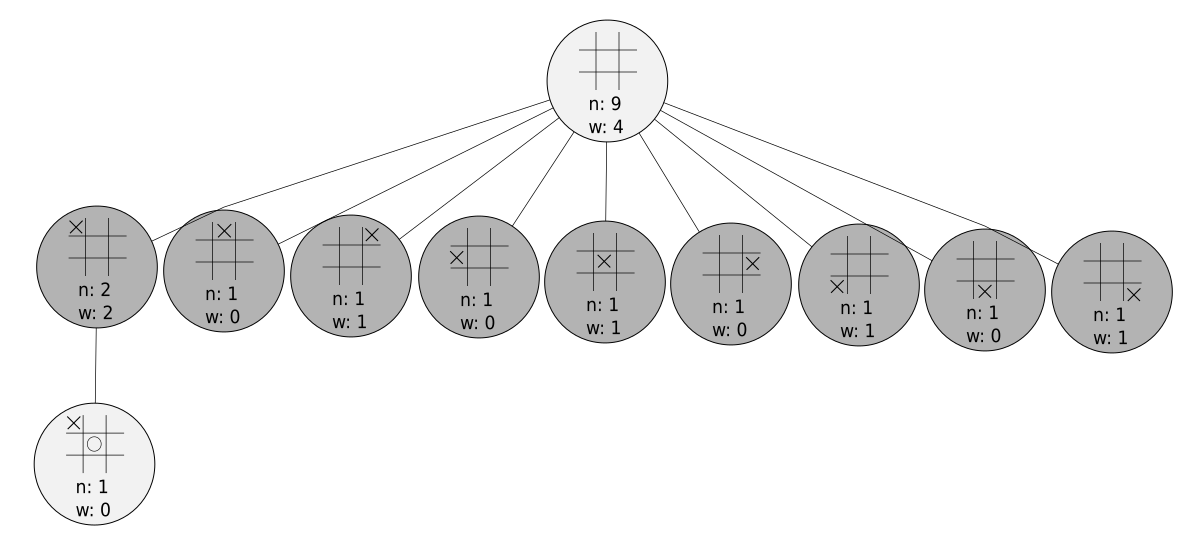
It’s important to note that these phases always begin with the current state of the board in the very top node. Now let’s imagine we chose $C$ such that the following node was selected:

As you can see, the node we selected doesn’t have any child nodes in the game tree. When this happens, we move into the expansion phase.

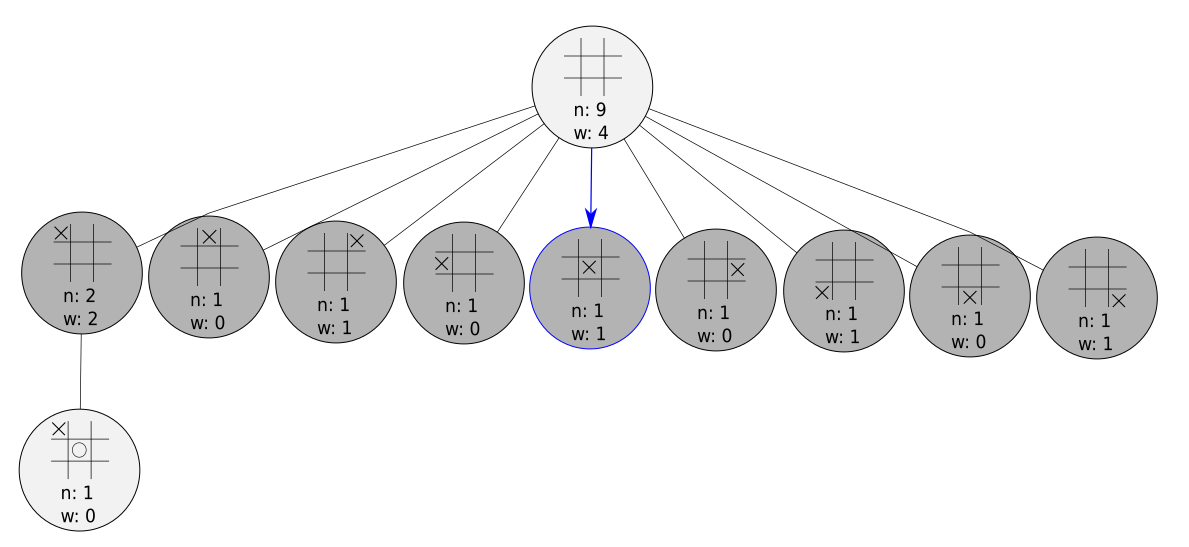
Expansion

HAL doesn’t have enough information to select a node anymore, so we grow our tree! Here we’ll just choose an action at random - this is called a light rollout.

In more complex games, it is common to use heavy rollout - this means using some deep heuristic knowledge to choose an action, or even a neural net trained to evaluate board position. This can lead to faster convergence to a more optimal tree. If the game’s not over yet, we move through to the simulation phase.

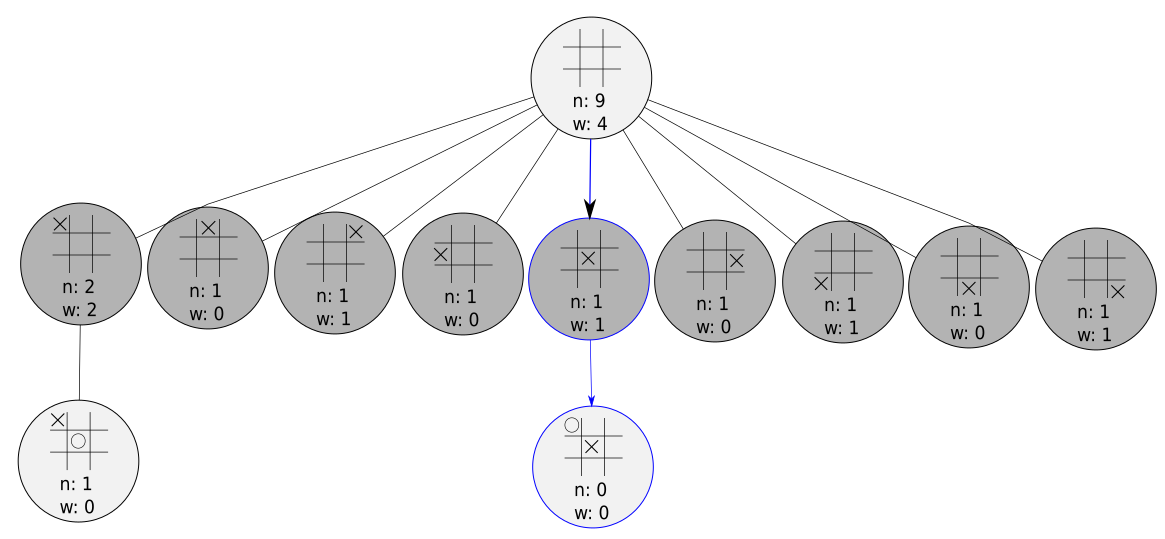
Simulation

At this point, we just simulate the game from our current node to the end and see who won! Actions along the simulation are chosen randomly. It’s important to note that we do not add states visited in the simulation phase to our game tree - the purpose of the simulation is just to help us evaluate the position of our current node.

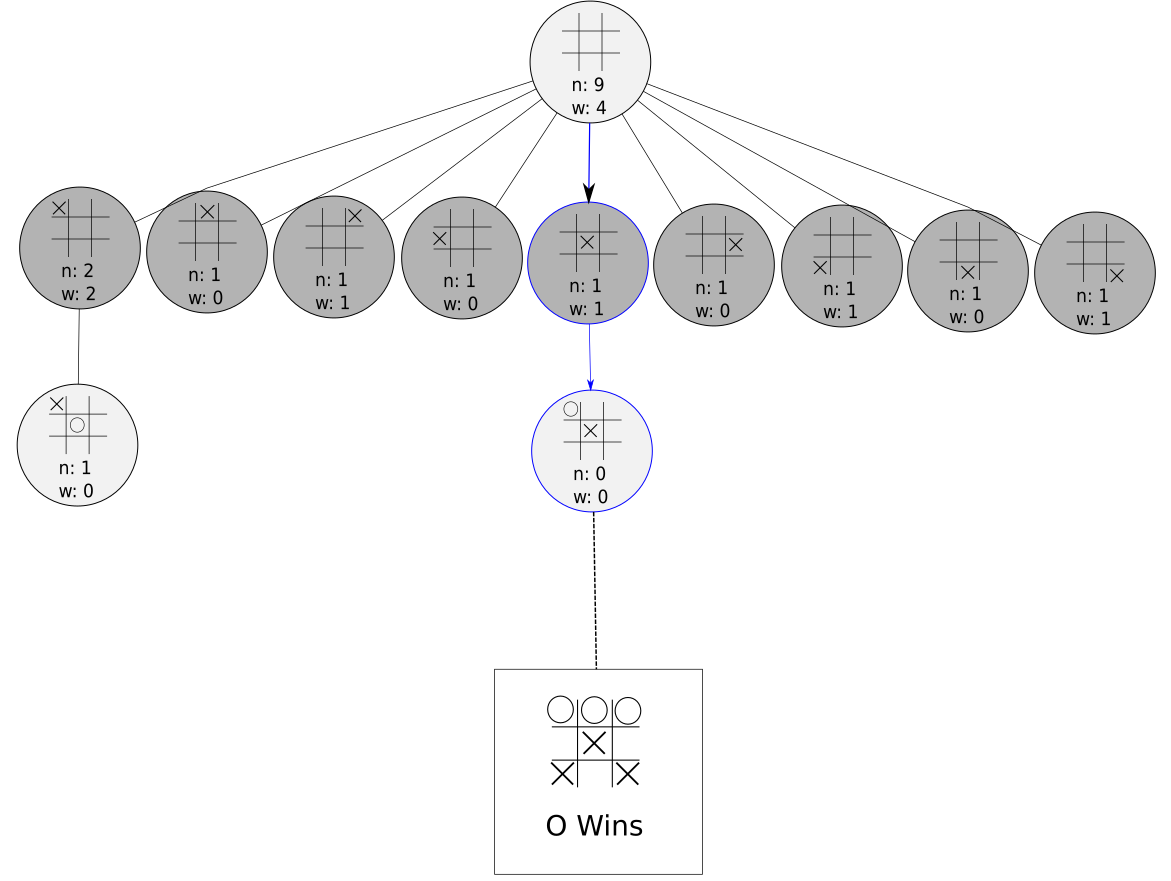
We’ve simulated out a game and O won it. Time to move to the next phase!

Backpropagation

In this phase, we simply update our selected nodes with the result of the simulation. We increment the visit count $n$ in each node, and we update our win count $w$ for only the light gray nodes.

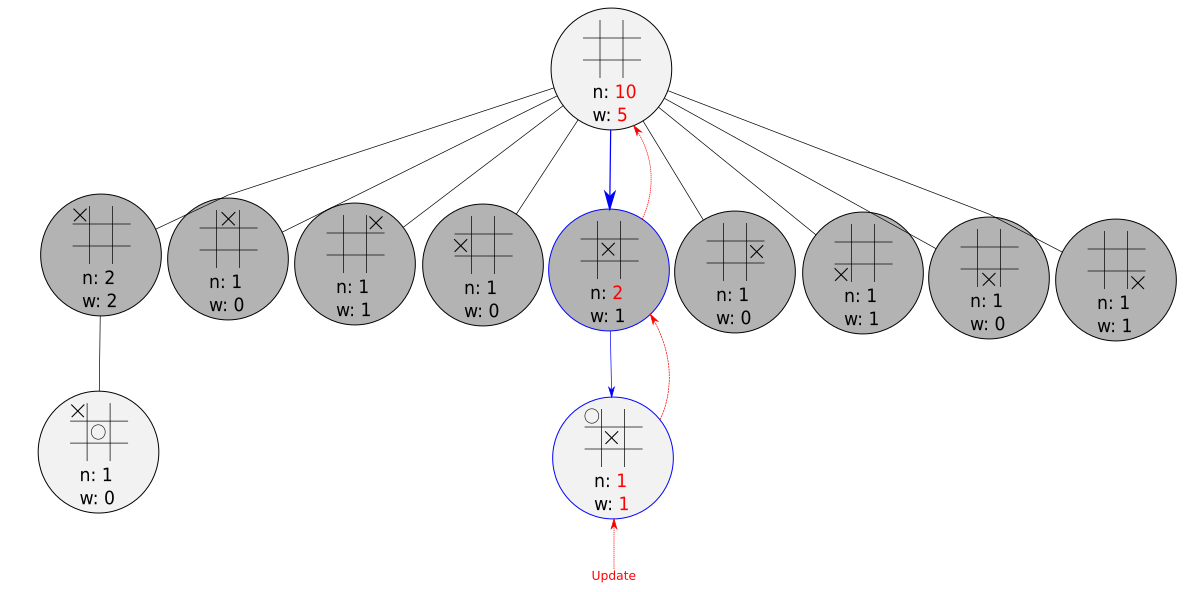
One simulation is noisy, and we can’t really be very certain of the results. But after hundreds or thousands of simulations, we start to get a clearer picture of what the value at each node might be.

Making a move

HAL still hasn’t even made his first move - this whole time HAL has just been thinking about which move he should make. After a couple of seconds, HAL has iterated through this 4-step process thousands of times, each node has had its win count and visit count update over and over again. I actually ran a MCTS on a simple tic-tac-toe environment, and here are the first couple nodes of the game tree:

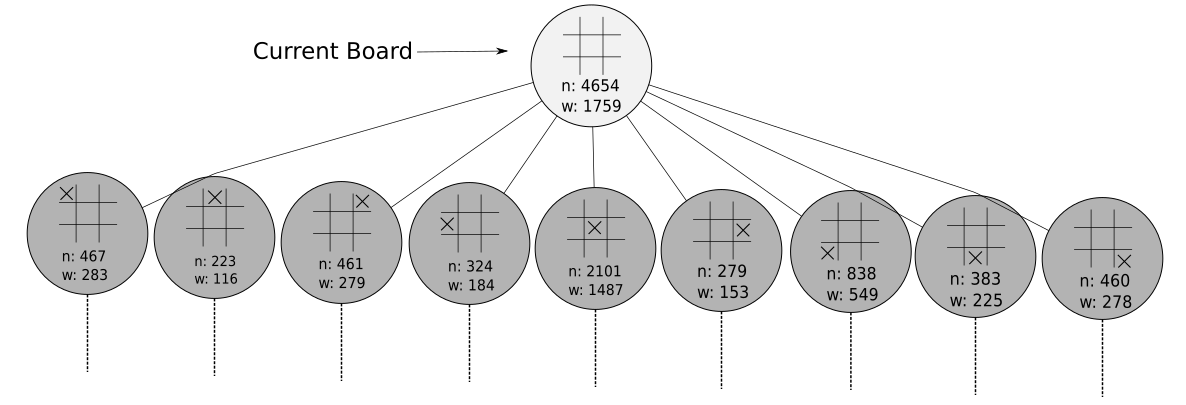
So which one does HAL pick? There are actually a few strategies here, and in most cases they all lead to the same answer. He can pick the action that leads to the node with the highest winning percentage or to the node with the highest visit count - the logic being that more interesting nodes are explored more. After HAL makes his choice, he’ll repeat this process over and over again until the end of the game.

And that’s it - the prolific Monte Carlo Tree Search! Thanks for reading!